Волновая природа атомных частиц

Лучи частиц и лучи света. Мы переходим теперь к самой поразительной, но и самой важной для понимания существа дела группе наблюдений. Они относятся к природе атомных частиц. Рассмотрим простейшую форму, в которой обнаруживаются атомные частицы, например электроны. Мы можем их наблюдать, когда они удалены из атома и свободно движутся в пустом пространстве. Если все электроны движутся в одном и том же направлении и с одинаковой скоростью, мы назовем их совокупность электронным лучом. Такие лучи возникают в любой радиолампе и, в частности, в телевизионной трубке. Они ударяются изнутри о телевизионный экран и создают изображение. Электронные лучи следует создавать в вакууме, так как в обычном воздухе электроны будут сталкиваться с молекулами воздуха, изменяя свое направление.

Можно было бы ожидать, что такие электронные лучи обладают очень простыми свойствами. Это группы частиц, движущихся по параллельным траекториям с одинаковой скоростью. Частицы движутся в пустом пространстве по прямым линиям; если они встречают препятствие, то рассеиваются по всем направлениям. Однако при их научении мы сталкиваемся с очень странными и неожиданными явлениями.

Прежде чем описывать эти явления, рассмотрим луч другого типа, луч света, например хорошо сфокусированный луч прожектора. Предположим далее, что наш луч имеет один цвет. Сравним оба эти луча. Мы ожидаем, что они совершенно различны. Световой луч — это пучок электромагнитных волн, распространяющихся в пространстве в определенном направлении; никакое вещество при этом не движется, изменяется только состояние электромагнитного поля в пространстве. Электронный же луч состоит из малых единиц материи, движущихся прямо вперед. Можно думать, что они так же отличаются друг от друга, как бегущая по озеру волна и плывущая в нем в том же направлении стая рыб.

Вспомним опыты, в которых мы продемонстрировали волновую природу света, в частности установку, в которой на пути луча было поставлено препятствие. Для света схема такого опыта показана на рис. 14, для электронного луча — на рис. 24.

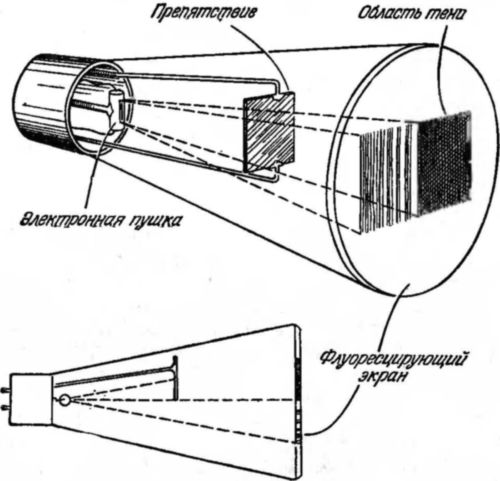
Рис. 24. Схема установки для наблюдения дифракции электронов, аналогичной установке для наблюдения дифракции света (рис. 14).

Последнюю схему можно считать идеальной для демонстрации различия между «лучом волн» и «лучом частиц». Если на пути «луча частиц» поставить препятствие, то ударившиеся о него частицы не попадут на экран, а частицы, прошедшие мимо экрана, достигнут его; те же частицы, которые пройдут у самого края препятствия, рассеются и отклонятся от своего пути. Следовательно, при использовании экрана, применяемого в телевизоре, мы увидим область тени и область света, с нерезкой границей между ними из-за рассеяния на краю препятствия. В отсутствие волн мы не ожидаем появления полос.

Как же были удивлены физики, когда они, выполнив этот опыт и ряд аналогичных опытов, нашли, что электронный луч проявляет волновые свойства, подобные волновым свойствам светового луча! На фото II была показана картина, которую дает световой луч в устройстве, изображенном на рис. 14. Она идентична картине, изображенной на фото IV и полученной на описанной выше установке (см. рис. 24).

Это лишь один из множества удивительных результатов, с несомненностью показавших, что электронный луч должен в какой-то степени обладать волновой природой; распространение пучка частиц, по-видимому, носит такой же характер, как и распространение волн. Движение электронов должно быть как-то связано с некоторой волной.

Количественное изучение полученной таким способом интерференционной картины позволяет измерить длину этой таинственной «электронной волны». Ее длина зависит от скорости электрона: чем больше скорость, тем меньше длина волны; для электронов с энергией в несколько электроновольт длина волны примерно равна размеру атома. Это действительно очень малая величина, и поэтому так трудно обнаружить волновую природу электронных лучей. В большинстве практических приложений электронных лучей (например, в телевизионных трубках) их волновая природа вообще не играет никакой роли.

Тем самым было сделано фундаментальное открытие — обнаружена волновая природа частиц. Полученный результат весьма поразителен и в высшей степени неожидан. Было выполнено множество экспериментов, прежде чем физики действительно убедились в том, что волновые эффекты не были вызваны какой-либо иной причиной. Однако все эти опыты делали все более ясным участие волн в движений электронов и других атомных частиц, например протонов.

Теперь возникает очевидный вопрос: как электрон может быть одновременно и частицей и волной? Волна — это нечто, непрерывным образом распределенное в пространстве, тогда как частица строго локализована. В любой момент частица находится здесь, а не там, а волна есть «натяжение» в пространстве, которое должно захватывать по крайней мере несколько длин волн, чтобы представлять то, что мы можем назвать волной. Можно ли сделать решающий опыт, чтобы получить однозначный и недвусмысленный ответ? Чем же в действительности является электрон — частицей или волной?

Это, вероятно, наиболее интересный вопрос современной физики. Но прежде чем обсуждать его, мы должны узнать самую поразительную вещь об электронных волнах, а именно то, что двойственная природа электронов как частиц и волн дает ключ к загадке строения атома! Неожиданные свойства электронов, вращающихся вокруг атомного ядра, прямо связаны с их волновой природой.

Свойства волн в ограниченном пространстве. Для того чтобы понять связь между электронными волнами и свойствами атомов, мы должны сначала изучить особенности поведения волн, распространяющихся в ограниченном пространстве.

Возьмем простейший пример — волны, бегущие по длинной веревке. Если веревка очень длинная, то мы можем создать бегущую волну, сообщая веревке небольшой, перпендикулярный ее направлению импульс. Если натянутая веревка привязана за один конец к неподвижному предмету, то импульс побежит по ней и в конце концов возвратится к нам, отразившись от того конца, где она привязана. Двигая соответствующим образом рукой, мы можем сообщить волне на веревке любую форму — по желанию сделать волну короткой или длинной. При прохождении длинной волны будут происходить медленные колебания, а при коротких волках веревка будет колебаться быстро. Теперь закрепим веревку между двумя близкими точками. При этом лучше рассматривать уже не веревку, а струну, натянутую между двумя точками, например струну на скрипке. Форма колебаний такой струны называется стоячей волной.

Теперь мы уже не можем получать любые частоты колебаний или любые длины волн. Действительно, можно возбудить только такие колебания, полуволна которых один, два или любое целое число раз укладывается в промежутке, разделяющем точки закрепления (рис. 25).

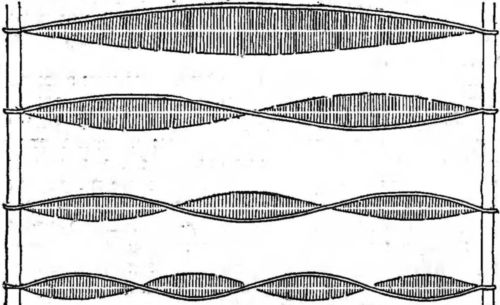
Рис. 25. Стоячие волны. Колебания струны, закрепленной в двух точках. Возникают только такие колебания, при которых между закрепленными точками укладываются только 1, 2, 3, 4 и т. д. полуволны. Горизонтальная прямая-положение струны в покое.

При постоянном натяжении струны определены не только формы колебаний, но и их частоты (числа колебаний в 1 сек). Каждое из различных колебаний, которые можно возбудить в такой струне, имеет свою характерную частоту, так что струна может колебаться только с одной из этого ряда частот. Наименьшая частота, возбудить которую легче всего, отвечает полуволне, в точности укладывающейся один раз на расстоянии между точками закрепления. Ее и получает скрипач, приводя струну в движение смычком. Однако можно возбудить и колебания высших порядков, так называемые флажолетные тона, при которых в струне укладываются две или большее число полуволн.

Даже когда звучит основной тон, движение струны не отвечает только колебаниям низшего типа. Истинное движение струны является комбинацией различных разрешенных типов движения. В действительности обычный музыкальный тон скрипки содержит известное количество высших частот, называемых гармониками. Их присутствие важно для красоты звука. Разница между игрой Пабло Казальса и игрой заурядного виолончелиста заключается в различной примеси высших частот. Но, какова бы ни была эта комбинация, в нее могут входить только те частоты, которые содержатся в наборе разрешенных комбинаций.

Данные, полученные нами при изучении струны, справедливы для волн всех видов. Если волны распространяются в ограниченном пространстве, мы видим систему волн определенных типов с рядом частот, характерных для данной системы. На этом основано большинство музыкальных инструментов. В струнных инструментах используются ряды дискретных частот, характерных для колебаний данной струны. В духовых инструментах используются определенные частоты воздушных волн, заключенных в трубе, будь то тромбон или органная труба.

Другой интересный пример таких волн легко увидеть при наблюдении волн на воде, распространяющихся в ограниченном пространстве, например в стакане. Поразительную картину можно обнаружить, наблюдая за поверхностью воды в стакане. В летящем винтовом самолете, когда частота колебаний мотора становится равной одной из возможных частот колебаний воды в стакане, становится заметной специфическая картина поверхностных волн. При изменении частоты дрожания мотора или при изменении количества воды в резонанс с дрожанием приходят другие колебания. Бы увидите колебания с характерными частотами, которые связаны с определенными волновыми картинами.

Вполне возможно рассчитать форму этих картин и предсказать, при каких частотах следует ожидать их появления. Для этого нужно только знать форму и размер стакана и свойства волн на поверхности воды.

Электронные волны и квантовые состояния. Вернемся теперь к электронным волнам. Как можно ограничить в пространстве электронные волны и наблюдать явления, подобные описанным? В любой ситуации, ограничивающей движения электронов, будут ограничены и электронные волны. Такая ситуация возникает, например, тогда, когда электрон находится близко от атомного ядра. Положительный заряд ядра притягивает электрон и мешает ему покинуть область, непосредственно примыкающую к ядру; движение электрона ограничено пространством, близким к ядру. Как это скажется на электронных волнах? Такой вопрос, поставил Эрвин Шредингер в 1926 г., и он же ответил на него.

Ему удалось рассчитать форму и частоты характеристических волновых картин, которые получаются, когда электрон привязан к ядру. Если известна связь между длиной электронной волны и скоростью электрона, это сводится к простой задаче динамики стоячих волн. Результат дает ряд отдельных колебаний, из которых каждое отвечает определенной волновой картине и определенной частоте. Волновая природа электрона сразу же «объясняет», почему электрон в атоме может обладать только определенными формами движения.

Этот результат имеет фундаментальное значение.

Он дает связь между волновой природой электрона и существованием дискретных состояний в атоме. Здесь мы коснулись самого существа природы. Если электрон может двигаться только в ограниченном пространстве вблизи ядра, то его волновые свойства разрешают лишь вполне определенные, заданные формы движения. Поэтому атом не может изменять свое состояние непрерывно, он должен переходить скачком из одного разрешенного состояния в другое.

Атом будет оставаться в состоянии с наименьшей энергией до тех пор, пока он не получит достаточно энергии, чтобы подняться в следующее состояние, как это и наблюдалось в опытах Франка и Герца.

Успех электронно-волновой модели атома особенно замечателен тем, что она позволяет количественно объяснить все детали наблюдаемых фактов. Шредингер сначала решил простейшую задачу о водородном атоме, в котором к ядру «привязан» только один электрон. Он получил ряд колебательных состояний, во всех отношениях отвечающих наблюдаемым квантовым состояниям водородного атома. В частности, частоты колебаний электронной волны в точности соответствуют энергиям квантовых состояний, если воспользоваться при этом знаменитой формулой Планка, связывающей энергию с частотой. Соответствующая энергия Е всегда равна частоте ? (омега), умноженной на постоянное число h, т. е. Е — h?. Число h — это так называемая постоянная Планка[34].

Точность результатов, вытекающих из этого соотношения, почти неправдоподобна! Шредингер вычислил частоты колебаний электронной волны, ограниченной притяжением. Он умножил эти частоты на постоянную Планка и получил — с точностью до последнего десятичного знака — энергии квантовых состояний водорода, разрешенные значения энергетического «банковского счета» водородного атома[35]. Очевидно, что волновая природа электрона должна служить решающим фактором для понимания свойств атома.

Ограничение электронных волн в пространстве обусловливает существование ряда разрешенных состояний и предписанных частот. Если вспомнить соотношение между частотой и энергией, то мы получим ряд состояний с разрешенной энергией. Состояние с наименьшей частотой является важнейшим, потому что оно обладает наименьшей энергией; это нормальное состояние атома. В таком состоянии волновая природа проявляется наиболее отчетливым образом. Ограниченные в пространстве электронные волны в атомах нельзя наблюдать непосредственно. Можно измерить их длину, частоты (точнее, разности между частотами, определяемые как разности энергий) и другие косвенные параметры. Но весьма поучительно видеть изображения электронных волновых картин. Это не фотографии, снять их, как мы дальше увидим, невозможно, а модели, построенные на основании вычислений. На фото V показаны картины электронных волн, или электронные конфигурации, расположенные в порядке возрастания частоты или энергии, для последовательных квантовых состояний электрона, движение которого ограничено притяжением к ядру. Самое низшее, или основное, состояние является вместе с тем и самым простым: чем выше частота, тем сложнее картина. Основное состояние сферически симметрично. Следующие состояния имеют вид «восьмерки». Более высокие состояния обычно имеют более сложный вид, хотя среди них встречаются и относительно простые.

Эти картины чрезвычайно важны, как фундаментальные формы, по которым строится вещество. Это формы, и притом единственно возможные, которые может принимать «движение» электрона в условиях, господствующих в атоме, т. е. под влиянием центральной силы (притяжение к ядру), связывающей электрон. Следовательно, подобные картины символизируют способ, которым природа связывает все нас окружающее и придает ему форму.

Картины на фото V и присущая им симметрия определяют поведение атомов, на них основано упорядоченное расположение атомов в молекулах и симметричное расположение их в кристаллах. Совершенство кристаллов отражает в большем масштабе фундаментальные формы атомных картин. В конечном счете все закономерности формы и строения, которые мы видим в природе, начиная от гексагональной симметрии снежинок и до сложной симметрии живых форм в цветах и животных, основаны на симметрии атомных картин.

Рассматривая эти картины, мы замечаем, что, чем выше частота (или энергия), тем мельче структура картины, тем меньше расстояния между гребнями и впадинами волн. Длина волны уменьшается. При переходе к очень высоким частотам (энергиям) структура картины становится столь мелкой, что она выглядит почти непрерывной. Следовательно, описываемое ею движение будет почти таким же, как и у обычной частицы, лишенной волновых свойств. Мы снова убеждаемся в том, что наша волновая картина точно воспроизводит ситуацию в атоме. При больших энергиях квантовые явления становятся несущественными и атом ведет себя, как обычная планетная система. Переход к «плазменным» условиям при большой энергии тоже объясняется волновой природой электрона.

Атом водорода в своем основном состоянии колеблется в соответствии с простейшей из возможных картин (см. первый снимок фото V).

Другие атомы, однако, даже в своих основных состояниях дают более сложные картины. Это стало понятным после того, как Вольфганг Паули сформулировал в 1927 г. весьма важный принцип. Он гласит, что если в атоме находится больше одного электрона, то каждый из них должен создавать различные картины. Поэтому при добавлении электрона должна возникать следующая (по порядку) конфигурация. Основное состояние сложного атома соответствует возбужденному состоянию более простого.

Здесь мы находим объяснение тому, что прибавление или удаление одного электрона так сильно сказывается в атомном мире. Картина, обусловленная последним электроном, определяет конфигурацию всего атома. Это в свою очередь определяет способ, которым соединяются атомы, т. е. то, образуют ли они кристалл, жидкость или газ. Наблюдаемая картина может заметно изменяться при переходе от некоторого числа электронов к ближайшему большему (см. фото V).

В мире атомов количество переходит в качество, одним электроном больше — и свойства полностью изменяются.

Открытое Шредингером фундаментальное значение электронных волн для строения атома и развитие этой теории Гейзенбергом, Максом Борном и Паули составили поворотный пункт в понимании природы человеком, сравнимый с ньютоновским открытием всемирного тяготения, электромагнитной теорией света Максвелла и теорией относительности Эйнштейна. Свойства атома, казавшиеся столь странными и непонятными на основе планетарной модели, нашли свое место в рамках волновой теории. Стоячая волна принимает некоторые определенные формы и частоты, так же как колебания воздуха в органной трубе, колебания скрипичной струны или дрожание водной поверхности в колеблющемся стакане. Всем этим колебаниям соответствует ряд волновых картин, начиная с самой простой, в которой колебания происходят с наименьшей частотой, и кончая более сложными картинами с высокими частотами. То же относится и к электронным волнам в атоме.

На основе этого нового понимания природы мы можем понять три замечательных свойства атома, перечисленные в конце предыдущей главы. Устойчивость атомов обусловлена тем, что для перехода от простейшей картины к более сложной необходимо сообщить им значительное количество энергии[36]. Пока количество сообщаемой атому энергии меньше указанного, сам атом остается в наинизшей конфигурации, которая, таким образом, отвечает наибольшей устойчивости. Тождественность атомов обусловлена тем, что волновые картины всегда одинаковы и определяются способом ограничения волны в пространстве. Один атом натрия тождествен другому потому, что во всех атомах электронная волна ограничена теми же условиями, т. е. притяжением ядра и электрическим действием других электронов в атоме. Тождественность двух атомов золота обусловлена тем, что одинаковое число электронов связано одним и тем же зарядом в центре, и поэтому эти электроны совершают одинаковые волновые движения. Наконец, воспроизводимость, т. е. способность возвращения к исходной форме после воздействия, как раз совпадает с той, которую и следует ожидать для случая волновых явлений, обладающих устойчивостью. При восстановлении исходных условий колебания электрона снова должны происходить так же, как и до воздействия, поскольку они однозначно определяются условиями, при которых движется электрон, и совершенно не зависят от того, что происходило ранее. Наблюдаемые конфигурации вообще не зависят от предыстории атома; мы можем разрушить атом, удаляя несколько электронов, или деформировать его, конденсируя наше вещество до твердого состояния (как это делалось в примере с натрием в предыдущей главе), но, как только атом вернется в исходные условия, электронные волны примут ту же форму, какую они имели вначале. Существует только одна конфигурация с наименьшей частотой (или энергией).

Замечательно, что мы на самом деле нашли в мире атомов то, что Пифагор и Кеплер тщетно искали в движении планет. Они полагали, что Земля и другие планеты движутся по особым орбитам, единственно возможным для каждой планеты и определенным каким-то основным принципом, не зависящим от частной судьбы и предыстории нашей планетной системы. Такой принцип отсутствует в движении планет, но он существует в движении атомных электронов это волновой принцип. Мы вспомним здесь пифагорейскую гармонию мира: квантовые состояния атома имеют предопределенные конфигурации и частоты. Каждый атом водорода во Вселенной задевает одну и ту же струну, колебания которой определяются набором характеристических частот. Здесь «гармония сфер» вновь появляется в мире атомов, но на этот раз под нею понимаются колебательные явления в стоячих электронных волнах (рис. 26).

Рис. 26. Гармония сфер по Кеплеру.