Принцип учета уровня владения языком обучения

Принцип учета уровня владения языком обучения отражает закономерную связь между эффективностью педагогической системы и учетом уровня владения учащимися языком обучения при проектировании и реализации процесса обучения. Эта закономерность обусловлена изучением общенаучных дисциплин параллельно с овладением языком обучения. Принцип учета уровня владения языком обучения требует строить процесс обучения на неродном для учащихся языке в соответствии с уровнем владения учащимися языком обучения.

На каждом этапе обучения иностранный учащийся обладает ограниченным арсеналом языковых средств и речевых способов восприятия и предъявления информации. В то же время, обучение общенаучным дисциплинам происходит в процессе учебно-научного общения, и для эффективного обмена информацией преподавателю необходимо использовать адекватные средства и способы презентации учебного материала. Принцип учета уровня владения учащимися языком обучения требует лингвометодического оформления занятий и учебных пособий по общенаучным дисциплинам в соответствии с уровнем владения языком, то есть в соответствии с этапом изучения языка. Например, авторам учебных пособий на неродном для учащихся языке рекомендуют учитывать «уровень сформированности ‹…› навыков и умений по русскому языку к каждому из этапов обучения» (Теория…, 1998, с. 16).

К сожалению, нельзя сказать, что это положение в достаточной степени реализовано в существующих учебных текстах для иностранных учащихся. Например, в учебнике по математике (Математика, 1987) для учета уровня владения языком использованы весьма скудные средства. Так, изложение начинается параграфами 1 и 2, в которых предъявлена информация о том, как читать числа, дроби, основные математические знаки и арифметические действия. Для этих параграфов характерно наличие текстовых единиц «Как читать…?» и «Говорим…» (в чем, кстати, принципиальное различие, ни студенту, ни преподавателю не пояснено, а по смыслу употребления в тексте учебника оно не просматривается, так как, по-видимому, его и нет).

С третьего параграфа начинается изложение собственно курса математики и стиль изложения меняется. С лингвометодической точки зрения характерной чертой этих текстов является предельно адаптированный язык, употребление относительно небольшого числа систематически повторяемых упрощенных синтаксических конструкций типа «… – это…», «если…, то…», «при… нужно…» и т. п. Отступления от собственно математического изложения вроде «читают…» становятся эпизодическими, в учебном тексте никак не выделенными и иногда просто неудачными. Например (Математика, 1987, с. 11): «Пропорция – это равенство двух отношений: a: b = c: d, где a, b, c, d – любые числа, но b № 0, d № 0. a, d – крайние члены пропорции; b, c, – средние члены пропорции. Читают[53]: «а» так относится к «бэ», как «цэ» относится к «дэ»». Что так читают?

Вообще говоря, в обсуждаемом учебнике сделана попытка различной лингвометодической организации текста соответственно этапу изучения русского языка. Если в параграфах 1 и 2 это, по сути дела, ввод и семантизация новой лексики (соответствует задачам начального курса), то каждый из параграфов 3–80 снабжен списком слов и словосочетаний с проставленными ударениями. Эти лексические единицы прежде всего должен усвоить иностранный учащийся. И лишь в параграфах 81–122, соответствующих третьему этапу изучения русского языка, элементы лингвометодического аппарата вообще в явном виде не присутствуют.

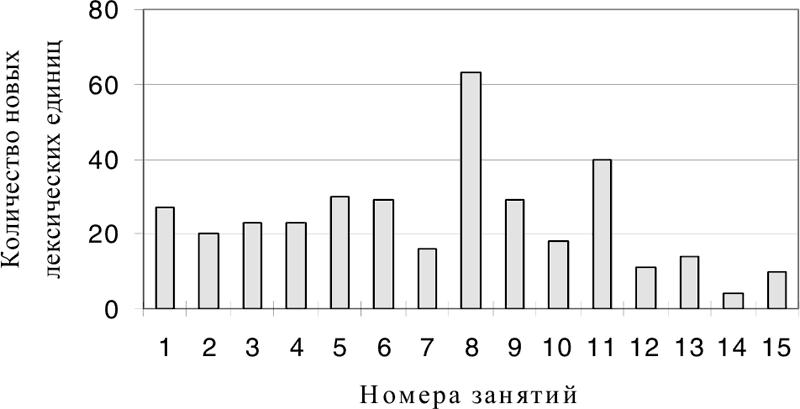
Рис. 24. Зависимость количества новых лексических единиц, вводимых на первых занятиях курса математики на неродном языке (по: Начальный…, 1988), от номера занятия

Хотя авторов данного учебника при всем желании никак нельзя упрекнуть в чрезмерном использовании лингвометодических средств, приведенный выше пример все-таки положительный. Гораздо легче найти примеры отрицательные, то есть фрагменты учебных текстов, в которых уровень владения учащимися языком обучения вообще не принимается во внимание. Разберем некоторые из них. На рис. 24 приведена гистограмма количества новых лексических единиц, вводимых на занятиях начального курса математики (Начальный…, 1988). Видно, что на восьмом занятии вводится почти в 3 раза больше новых слов и словосочетаний, чем в среднем по начальному курсу. Даже не вникая в детали, можно сделать вывод о том, что занятие составлено с нарушением принципа учета уровня владения языком обучения: учащиеся на 8–10-й неделе изучения русского языка не готовы воспринять такое количество новых лексических единиц за одно занятие. Вообще говоря, следует отметить, что в пособии (Начальный…, 1988) по крайней мере занятия 1–6, 8, 9, 11 (9 занятий из 15) составлены с явным нарушением рекомендаций психологов, утверждающих, что взрослый учащийся при изучении иностранного языка в состоянии активно усвоить за одно занятие не более 12–15 новых лексических единиц. Но это в условиях изучения языка, а не обучения на изучаемом языке. Последняя ситуация целенаправленно вообще не изучалась, но, во всяком случае, при обучении на неродном языке максимальное число новых лексических единиц на одно занятие должно быть заметно меньше 12–15.

На рис. 25 приведена гистограмма зависимости количества вводимых новых лексических единиц от номера занятия, построенная для более удачного в рассматриваемом отношении «Введения в математику на русском языке как иностранном» (Левина, Сурыгин, 1995). Для удобства сравнения гистограмма построена в тех же осях, что и гистограмма на рис. 24. Из гистограммы видно, что во «Введении в математику…» только одно, первое, занятие не удовлетворяет рекомендациям психологов по количеству вводимой лексики. Но такое распределение нового лексического материала обоснованно, так как именно на первом занятии формируется основа информационного канала и лексика этого занятия постоянно активизируется в ходе последующих занятий.

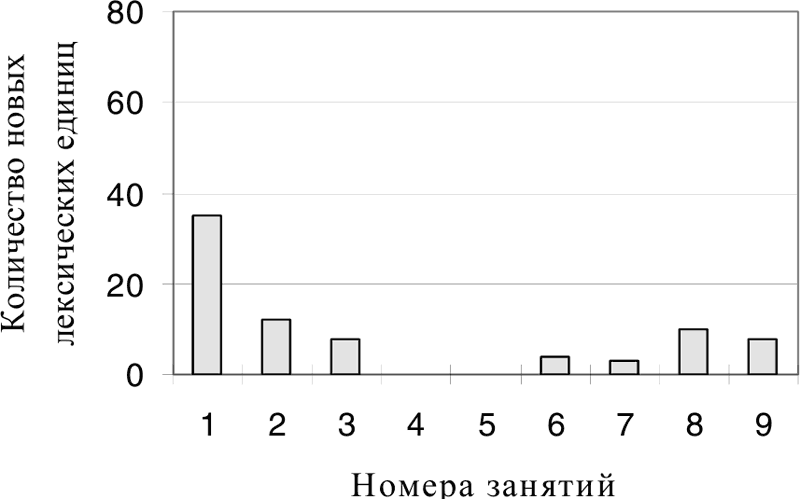
Рис. 25. Зависимость количества новых лексических единиц, вводимых на первых занятиях курса математики на неродном языке (по: Левина, Сурыгин, 1995), от номера занятия

Рассмотрим примеры использования недостаточно адаптированного языка. «Определение. Числа, записываемые[54] в виде…» (Шишкин, Евсин, Корнева, 1984, с. 24). И это практически в начале курса, когда иностранные студенты еще почти не владеют русским языком! Это предложение в учебнике для иностранцев надо строить, например, так: числа, которые можно записать в виде… или числа, которые записывают в виде…

Приведем более тонкий пример. В «Основы…» (ч. 3, 1993, с. 4) читаем: «Определение. Равносильные уравнения – это уравнения, у которых области определения равны и множества решений совпадают[55]». В учебной книге для российских студентов такая формулировка может быть приемлема с точки зрения литературного стиля, но не с точки зрения математики: понятие „совпадение множеств“ не определено. Тем не менее, российскому студенту понятно, что слова равны и совпадают в данном контексте употреблены как синонимы. Но как догадаться об этом иностранному студенту, которому такая формулировка создает дополнительные трудности? Этот пример является хорошей иллюстрацией к тезису о том, что использование различных лексических единиц, грамматических конструкций для обозначения одного и того же понятия затрудняет понимание и усвоение учебного материала учащимися. По-видимому, данное определение желательно сформулировать так: «Определение. Равносильные уравнения – это уравнения, у которых равны области определения и равны множества решений».

Рассмотрим особо проблему определений в учебной книге на неродном для студента языке. На самом деле эта проблема гораздо шире, она затрагивает не только определения, но и формулировки теорем, и вообще язык учебных текстов, причем не только на неродном для учащихся языке (Гомоюнов, 1993, 1996; Кесаманлы, Кесаманлы, Коликова, 1999; Кузнецова, 1997). При анализе проблемы определений будем исходить из методологического положения о том, что форма содержательна и использование различных грамматических форм для обозначения однородных предметов мысли методически необоснованно (Гомоюнов, Кесаманлы, Коликова, 1997).

Известно, что в вузовских учебниках по математике определения дают в совершенно различной форме. Это создает дополнительные трудности даже для российских студентов, у которых вследствие различного языкового оформления однотипных математических утверждений может происходить смещение центра трудности при изучении математики. Это совершенно недопустимо в учебных книгах на неродном для учащегося языке, особенно в пособиях для начального этапа обучения. Если и ставить задачу подготовки иностранного студента к чтению недостаточно лингвистически проработанной учебной литературы, то делать это надо очень постепенно и, конечно, по возможности на более поздних этапах изучения языка как средства обмена учебной и научной информацией. А что мы видим, например, в уже цитированном учебнике (Математика, 1987)?

Сначала определения вводятся через синтаксическую конструкцию «… – это…», что совершенно естественно. Но приведем несколько примеров.

«Натуральные числа, противоположные им числа и число нуль – это целые числа» (с. 7) (определяемое понятие стоит в конце). Через две строки – следующее определение: «Рациональное число – это число, которое можно написать в виде m/n» (с. 8) (определяемое понятие – в начале). На той же странице: «Модуль числа – его абсолютная величина» (опущено привычное уже студенту это).

На стр. 15 очередное определение формулируют уже с помощью синтаксической конструкции со словом если: «Множество задано, если известно свойство, которое имеют элементы этого множества»[56] (можно было: Задать множество – это задать свойство элементов этого множества). «Два множества равны, если они состоят из одинаковых элементов» (с. 15) (можно было: Равные множества – это множества, которые состоят из равных элементов). Все на той же странице авторы используют новую синтаксическую конструкцию: «Множество, которое не содержит ни одного элемента, называется пустым множеством» (с. 15). Следующее определение ровно через две строки использует уже и глагол называться, и союз если: «Множество B называется подмножеством A, если каждый элемент множества B принадлежит множеству A» (с. 16). А еще через 10 строк для следующего определения используется опять новая синтаксическая конструкция: «Множества, элементы которых числа, – есть числовые множества» (с. 16).

Аналогично обстоит дело, например, и в учебных текстах по физике, что можно проиллюстрировать на примере учебника, допущенного Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов-иностранцев, обучающихся на подготовительных факультетах высших учебных заведений (Физика, 1983). Только среди определений, специально выделенных в тексте курсивом, и не принимая во внимание многочисленных контекстуальных определений, мы насчитали 15 различных грамматических конструкций. Справедливости ради следует сказать, что частота их использования существенно различна и в подавляющем большинстве случаев авторы используют лишь пять (см. табл. 9).

Но тогда тем более непонятно, зачем нужно вводить в текст (напомним – для иностранных учащихся) остальные 10 конструкций, которые все вместе использованы лишь примерно в 10 % определений. Обнаружить какую-либо систему в использовании различных грамматических конструкций не удается, ее нет. Довольно показательной иллюстрацией бессистемности является следующая выдержка:

«Совокупность нескольких материальных объектов в физике называют системой. В механике системой называют совокупность физических тел.

Таблица 9. Относительная частота использования синтаксических конструкций в определениях (учебник «Физика» 1983)

Силы взаимодействия тел данной системы называют внутренними силами. Силы, с которыми действуют на данную систему внешние тела, называются внешними силами.

Замкнутой системой называется система, на которую не действуют внешние силы»[57] (Физика, 1983, с. 87).

Этот отрывок содержит пять определений, для них использованы все четыре возможные конструкции с глаголом называть(ся) (вторая, четвертая, снова вторая, первая и, наконец, третья позиции в табл. 9). По-видимому, это оживляет текст, повышает его литературное качество, но вряд ли это оценят учащиеся, изучающие физику на неродном языке. Им такое разнообразие языковых средств, используемых для выражения однотипного содержания, к тому же сосредоточенных в небольшом фрагменте, лишь увеличивает трудности в понимании смысла написанного. Сколько дополнительных усилий понадобится учащемуся, изучающему физику на неродном языке, чтобы понять, почему в одном абзаце «силы взаимодействия тел данной системы называют внутренними силами», а «силы, с которыми действуют на данную систему внешние тела, называются внешними силами»?

Выше мы отметили, что в учебнике довольно значительна доля других конструкций определений, некоторые из которых совсем неудачны. Например, «если при переходе луча из одной прозрачной среды в другую луч меняет свое направление на границе, то такое явление называется преломлением света» (там же, с. 322). Корректнее (но в стиле того же учебника) построенная фраза, снабженная необходимыми типографскими выделениями, сразу становится значительно более легкой для восприятия: изменение направления распространения луча на границе прозрачных сред называют преломлением света.

А сколько времени и усилий потребуется изучающему физику на неродном языке, чтобы разобраться в таком определении, конструкция которого встречается в учебнике единственный раз: «тела называются электрически однородными, если их электрические свойства одинаковы в пределах всего объема» (там же, с. 193)? Придерживаясь стиля цитируемого учебника, для иностранных учащихся это определение можно было бы изложить в такой, например, редакции: тело, которое имеет одинаковые электрические свойства по всему объему, называют электрически однородным телом.

Такой разнобой в форме определений – одного из важнейших элементов научных знаний – свидетельствует об отсутствии сколько-нибудь серьезной лингвометодической проработки учебных текстов. И это обычное явление, которое недопустимо и в учебных книгах на родном языке, не говоря уже об учебниках для иностранных учащихся.

Конечно, проблема определений чрезвычайно сложна и в методологическом, и в лингвистическом, и в дидактическом аспектах, поэтому мы далеки от мысли требовать полной унификации формы определений, да это и невозможно. Тем не менее, мы считаем необходимым подчеркнуть, что по крайней мере в учебных текстах на неродном для учащихся языке использование тех или иных грамматических конструкций для определения терминов должно быть лингвометодически обоснованным и выверенным. И если уж не удается унифицировать структуру определений, теорем и т. п., в учебных текстах на неродном для учащихся языке необходимо делать, по крайней мере, две вещи. Во-первых, четко выделять определения типографскими средствами и, возможно, словом определение, хотя последнее принято далеко не во всех дисциплинах. Во-вторых, желательно выделять определяемый термин, чтобы его положение в предложении сразу становилось понятным читающему. К тому же, выделение определяемого термина в какой-то мере поможет избежать определений «оригинальной» и неоправданно сложной структуры, подобной приведенным выше. Все это и означает в данном случае учет уровня владения языком обучения.

Заканчивая обсуждение принципа учета уровня владения языком, отметим, что для методически обоснованного, адекватного выбора педагогических действий преподавателю необходима осведомленность о поэтапных требованиях к языковым знаниям, коммуникативным умениям и речевым навыкам, которые определены в программе по русскому языку. В помощь преподавателям сформулирована единая система требований к деятельности преподавателя по учету уровня владения учащимися языком обучения (единый языковой режим), описаны элементы необходимых преподавателям лингвометодических знаний (Методические…, 1996). Определенные ориентиры обозначены в учебных программах по общенаучным дисциплинам. Например, в программе по химии (1997) к каждой теме курса сформулированы предметно-речевые умения, которые необходимо сформировать у обучающегося на неродном языке. Среди предметно-речевых умений: давать определения, давать ответы на вопросы по теме, строить монологическое высказывание и т. п. Авторы программы по математике (1997) пошли по другому пути. Весь курс математики разбит на четыре этапа, которые соотнесены с характером математического материала и этапами изучения русского языка. Каждый этап изучения математики охарактеризован с точки зрения уровня владения учащимися языком обучения, даны рекомендации, на развитие каких предметно-речевых умений и на каких этапах целесообразно обращать внимание прежде всего. Однако цели в языковой области сформулированы общо, недостаточно конкретно и требуют диагностичной постановки. Тем не менее, несмотря на имеющиеся результаты, проблема требует дальнейшей разработки.

Итак, принцип учета уровня владения языком обучения реализуют в педагогической системе предвузовской подготовки иностранных учащихся:

– в языковом оформлении процесса обучения соответственно этапу изучения языка;

– в предметно-языковой координации (межпредметной координации в преподавании русского языка и общенаучных дисциплин);

– в выделении при изучении общенаучных дисциплин этапов, соотнесенных с этапами изучения языка (при сохранении целостности начальных этапов изучения и языка, и дисциплин);

– в требовании лингвометодической компетентности преподавателей.