Занятие 16 Логические задачи
1. Игра на внимание «Отвечай – не торопись!» (3 мин)
На доске записана схема «Виды логических задач»
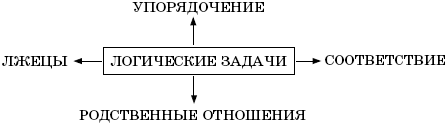
Затем учитель в произвольном порядке показывает на различные виды задач, а дети хором называют их местоположение на схеме: слева, справа, внизу, вверху.
Игра может проходить в быстром темпе на выбывание.
2. Решение логических задач на упорядочение (10 мин)
– Сегодня на занятии мы с вами будем учиться решать логические задачи. Логические задачи отличаются от обычных тем, что в них требуется не умение вычислять, а умение рассуждать… Логические задачи бывают разных видов, некоторые из них мы рассмотрим на этом занятии.
Учитель зачитывает текст задачи, дети хором отвечают.
Примеры задач:
• Петя старше Маши, а Маша старше Коли. Кто самый старший?
(Петя.)
• Серёжа выше Наташи, а Оля выше Серёжи. Кто самый высокий?
(Оля.)
• Ваня худее Миши, но толще Андрея. Кто самый худой?
(Андрей.)
• Катя иаее, чем Лиза. Лиза иаее, чем Лена. Кто иаее всех?
(Катя.)
• Прс веселее, чем Лвд. Прс печальнее, чем Ксн. Кто веселее всех?
(Ксн.)
• Вшф клмнее, чем Двт. Жкн клмнее, чем Вшф. Кто клмнее всех?
(Жкн.)
Лошадь ниже, чем кролик. Лошадь выше, чем жираф. Кто выше всех?
(?)
При решении «таинственных» задач (с непонятными словами) дети нередко вначале пытаются выяснить, расшифровать, что значат эти слова. Учитель показывает, что для нахождения ответа это не нужно. Последняя задача – «ловушка»: в ней логические выводы вступают в противоречие с реальностью. При решении подобных задач следует давать два ответа: один – формально-логический, вытекающий из условия; и второй – показывающий ошибочность первого ответа с позиций здравого смысла.
При решении задач на упорядочивание рекомендуется записывать условие со знаками «<» и «>» или использовать схемы. При этом знак «>» обозначает любой превосходящий признак: старше, выше, толще, веселее и т. д.
Далее учитель предлагает решить задачу на упорядочение (заранее написана на доске) и составить алгоритм решения подобных задач.
Задача:
«Ваня старше Пети. Дима младше Коли. Петя старше Коли. Ваня младше Юры. Кто старше всех?»
Вариант алгоритма решения:
1. Записать условие при помощи знаков: В>П, Д<К, П>К, В<Ю.
2. Привести все записи к единому виду: В>П, К>Д, П>К, Ю>В.
3. Расставить по порядку: Ю>В, В>П, П>К, К>Д, или Ю>В>П>К>Д.
4. Ответить на вопрос задачи: Юра – самый старший.
Полученный алгоритм предлагается использовать для самостоятельного решения более сложной задачи на упорядочение.
Задача (заранее написана на доске):
«Возле почты растут 6 деревьев: сосна, берёза, липа, тополь, ель и клён. Какое из деревьев самое высокое и какое самое низкое, если известно, что берёза ниже тополя, липа выше клёна, сосна ниже ели, липа ниже берёзы, сосна выше тополя?» (Ель – самое высокое дерево, клён – самое низкое.)
3. Решение логических задач: родственные отношения (5 мин)
Учитель предлагает 5–6 задач «про родственников» (можно в виде упражнения «Проверь себя»).
Примеры логических задач:
• Отца одного человека зовут Николай Петрович, а его сына – Алексей Владимирович. Как зовут этого человека?
(Владимир Николаевич.)
• Шли по улице два отца, два сына и дед с внуком. Видят, мороженое продают. Купили 3 порции, и каждому по одной досталось. Как такое могло быть?
(Всего было 3 человека: дедушка, его сын и внук. Но дедушка при этом является отцом для своего сына, а его сын – отцом для внука.)
• Иван Петрович – отец Нины Ивановны, а Катя – дочь Нины Ивановны. Кем приходится Катя Ивану Петровичу?
(Внучкой.)
• Возможно ли такое предложение: «Ты мне сын, но я тебе не отец»?
(Да, если это произносит мать.)
• В семье несколько детей. Один ребёнок говорит, что у него есть брат и сестра. Другой ребёнок говорит, что у него нет сестры. Сколько в семье детей? Сколько мальчиков и сколько девочек?
(Трое: два мальчика и девочка.)
• Иванова спросили, кто изображён на портрете в его комнате. Иванов ответил: «Отец изображённого на картине лица является единственным сыном того, кто это говорит». Чей это портрет?
(Внука.)
• Отец сказал, что у него 7 сыновей. У каждого сына есть одна сестра. Сколько всего детей в семье?
(8: 7 сыновей и 1 дочь.)
• Ольга Сергеевна и Елена Сергеевна – дочери Сергея Павловича. Никита – сын Ольги Сергеевны. Кем ему приходится Елена Сергеевна и Сергей Павлович? В каких родственных отношениях между собой Ольга Сергеевна и Елена Сергеевна?
(Тётей; дедушкой; сёстры.)
4. Решение логических задач на нахождение соответствия (5–6 мин)
На доске записана задача:
«В соревнованиях по бегу Серёжа, Гриша и Коля заняли три первых места. Какое место занял каждый, если известно, что Гриша занял не второе и не третье место, а Серёжа не третье?»
– Подобные задачи удобнее решать, используя таблицу.
(Учитель на доске, а дети в тетради рисуют и последовательно заполняют таблицу.)
– В строчках записывается, о ком или о чём задача, в столбиках – что нужно узнать.

– Ещё раз читаем задачу и заполняем таблицу знаками «+» (да), «—» (нет), исходя из данных условия: на пересечении клеток «Гриша» и «2-е место» ставим «—», «Гриша» и «3-е место» ставим «—», «Серёжа» и «3-е место» ставим «—».
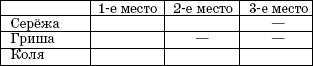
– Затем последовательно заполняются остальные клетки после анализа полученных данных: если в двух клетках из трёх стоит «—», значит, в пустой клетке надо поставить «+»; если в одной клетке стоит «+», значит, во всех остальных клетках тех же строчки и столбика нужно ставить «—».

– После того как все клетки таблицы заполнены, можно ответить на вопрос задачи: Гриша занял первое место, Серёжа – второе, а Коля – третье.
Желательно устно составить краткий алгоритм решения задачи.
Например:
Шаг 1. Построить таблицу.
Шаг 2. Обозначить «+» и «—» то, что известно по условию.
Шаг 3. Заполнить оставшиеся клетки.
Шаг 4. Вывод – решение задачи.
5. Работа в группах «Решение задач» (7–8 мин)
Каждая группа получает текст задачи и пустую таблицу для записи данных. Возможен вариант, когда несколько групп получают одинаковые задачи.
Примеры задач (несколько групп получают одинаковые):
• Беседуют трое друзей: Степанов, Иванов, Петров. Ваня сказал Степанову: «Любопытно, один из нас Иван, другой – Пётр, третий – Степан, но ни у кого имя не соответствует фамилии». Как звали каждого друга?
(Степанов Пётр, Иванов Степан, Петров Иван.)
• Света, Марина, Андрей, Кирилл и Юра держат домашних животных. У каждого либо кошка, либо собака, либо попугай. Девочки не держат собак, а мальчики – попугаев. У Светы нет кошки. У Светы и Марины разные животные. У Марины и Андрея – одинаковые. У Андрея и Кирилла – разные. У Кирилла и Юры – одинаковые. Какие животные у каждого?
(У Светы – попугай, у Марины – кошка, у Андрея – кошка, у Кирилла – собака, у Юры – собака.)
• В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке. Лимонад стоит между кувшином и квасом. В банке не лимонад и не вода. Стакан стоит между банкой и молоком. В каком сосуде находится каждая из жидкостей?
(Молоко в кувшине, лимонад в бутылке, квас в банке, вода в стакане.)
Комментарий к ответу: иногда возникает затруднение: какую информацию несёт, например, предложение: «Лимонад стоит между кувшином и квасом». Ответ: «Это значит, что лимонад находится не в кувшине и квас тоже находится не в кувшине».
Можно предложить дополнительное задание: узнать, в каком порядке расположены жидкости.
При подведении итогов группы, решавшие одинаковые задачи, объединяются для проверки решения. Коллективного обсуждения задач можно не проводить.
6. Решение логических задач про лжецов (4–5 мин)
– На одном острове живут два племени: рыцари, которые, всегда говорят правду, и лжецы, которые всегда обманывают.
Представьте себе, что вы оказались на этом острове и попали в несколько затруднительных ситуаций. Постарайтесь их разрешить.
Примеры логических задач:
• Вы встретили жителя острова. Какой вопрос ему нужно задать, чтобы точно определить кто он: рыцарь или лжец?
(Любой вопрос, правильность которого очевидна. Например, «Какое сегодня число?», «Дома умеют летать?» и др.)
• Вы взяли жителя острова в проводники. Пошли и увидели другого жителя острова. Вы послали проводника узнать, кем является житель острова. Проводник вернулся и сказал, что житель говорит, что он рыцарь. Кем был проводник: рыцарем или лжецом?
(Любой житель острова на вопрос «Кто ты?» ответил бы: «Рыцарь», при этом рыцарь бы сказал правду, а лжец соврал. Если бы проводник был лжецом, он бы ответил, что житель – лжец. Но так как он сказал правду, то он – рыцарь.)
• Вы пришли в одну деревню и спросили прохожего: «Это ваша родная деревня?», на что тот ответил «Нет». Какая это деревня: рыцарей или лжецов, если вы не знаете, с кем разговаривали?
(Если бы это была деревня рыцарей, то любой прохожий ответил бы «Да». Значит, это деревня лжецов: рыцарь бы сказал правду, что он здесь не живёт, а лжец бы обманул и тоже ответил «Нет».)
• Вы встретили прохожего, который сказал: «Я лжец». Может ли такое быть?
(Нет, потому что рыцарь так про себя сказать не может, а лжец в этом случае говорит правду, что тоже не может быть. Это был путешественник с другого острова, который иногда говорит правду, а иногда обманывает.)
7. Подведение итогов занятия
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК